Если перед Вами встала задача отыскания производной некоторой функции одной переменной, то эта статья, несомненно, укажет направление решения. Здесь мы попытались представить общий взгляд на применение всей обширной теории дифференцирования к нахождению производной. Так как дифференцировать приходится функции с различным способом задания (в явном, неявном, параметрическом виде) и всякой степени сложности (основные элементарные, сложные, элементарные), то и подходы к решению подбираются в зависимости от ситуации.
В этой таблице собрана абсолютно вся информация, необходимая при дифференцировании функции. Немного поясним ее содержание.
В простейших случаях продифференцировать функцию можно с использованием определения производной, то есть, вычислив соответствующий предел. Этот метод можно назвать непосредственным дифференцированием.
Если Вам потребовалось найти производную одной из основных элементарных функций, то все они собраны в таблице основных производных и доказаны на основании определения. Так что смело пользуйтесь этой таблицей и держите ее перед глазами.
При нахождении производных суммы, разности функций, их произведения или отношения к Вашим услугам правила дифференцирования. Их приходится использовать почти в каждой задаче. Если к таблице производных и правилам дифференцировани добавить формулу нахождения производной сложной функции, то вмести они позволят дифференцировать любую элементарную функцию, заданную в явном виде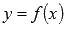 
.
.
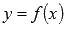Для дифференцирования показательно степенной функции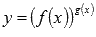 
очень удобно использовать логарифмическую производную. С ее помощью достаточно просто находятся и производные громоздких дробей.
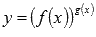очень удобно использовать логарифмическую производную. С ее помощью достаточно просто находятся и производные громоздких дробей.
Если функция представлена параметрическим способом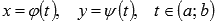 
, то ее дифференцирование подробно описано в разделе производная параметрически заданной функции.
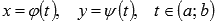, то ее дифференцирование подробно описано в разделе производная параметрически заданной функции.
Существует несколько способов дифференцирования неявно заданной функции вида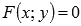 
. Можно найти производные от обеих частей равенства, считая y функцией от x, и разрешить полученное уравнение относительно производной. Производная неявно заданной функции также может быть найдена с использованием понятия частных производных.
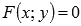. Можно найти производные от обеих частей равенства, считая y функцией от x, и разрешить полученное уравнение относительно производной. Производная неявно заданной функции также может быть найдена с использованием понятия частных производных.
Комментариев нет:
Отправить комментарий