Репетитор по математике не всегда может объяснить материал, который неудачно изложен в учебнике.
Ксожалению, таких тем становится все больше и больше, и ошибки изложения вслед за авторами пособий совершаются в массовом порядке. Это относится не только к начинающим репетиторам по математике и репетиторам по совместительству (репетиторы — студенты и репетиторы ВУЗов), но и к опытным преподавателям, репетиторам — профессионалам, репетиторам со стажем и квалификацией. Талант грамотного корректора шероховатостей школьных учебников имеют далеко не все репетиторы математики. Не все также понимают, что эти коррекции (или дополнения) необходимы. Адаптацией материала для его качественного восприятия детьми занимаются единицы. Ксожалению, ушло то время, когда преподаватели математики вместе с методистами и авторами изданий в массовом порядке обсуждали каждую букву учебника. Раньше, прежде чем пустить учебник в школы, проводили серьезные анализы и исследования результатов обучения. Пришло время дилетантов, стремящихся сделать пособия универсальными, подгоняя их под стандарты сильных математических классов.
Гонка за увеличением количества информации приводит только к снижению качества ее усвоения и, как следствие, к снижению уровня реальных знаний по математике. Но на это никто не обращает внимание. И наши дети вынуждены уже в 8 классе изучать то, что мы с вами проходили в институте: теорию вероятности, решение уравнений высоких степеней и кое-что еще. Адаптация материала в книжках для его полноценного восприятия ребенком оставляет желать лучшего и репетитор по математике вынужден как-то с этим бороться.
Поговорим о методике преподавания такой специфической темы, как «деление уголком многочлена на многочлен», более известной во взрослой математике как «теорема Безу и схема Горнера». Еще каких-нибудь пару лет назад вопрос не стоял перед репетитором по математике так остро, ибо он не входил в основную школьную программу. Теперь уважаемые авторы учебника под редакцией Теляковского внесли изменения в последнее издание лучшего, на мой взгляд, учебника, и, окончательно испортив его, только добавили репетитору лишних забот. Преподаватели школ и классов, не имеющих статус математических, ориентируясь на нововведения авторов, стали чаще включать дополнительные параграфы в свои уроки, а любознательные дети, рассматривая красивые странички их учебника математики, все чаще спрашивают репетитора: «Что это за деление уголком? Мы будем это проходить? Как делить уголком?» От таких прямых вопросов уже не спрятаться. Репетитору придется что-то рассказывать ребенку.
А как? Наверное, я бы не стал описывать метод работы с темой, если бы в учебниках она грамотно преподносилась. У нас ведь как все происходит? Учебники нужно печатать и продавать. А для этого их надо регулярно обновлять. Преподаватели Вузов жалуются, что дети приходят к ним с пустыми головами, без знаний и навыков? Требования к математическим знаниям растут? Отлично! Давайте мы уберем некоторые упражнения, а вместо них вставим темы, которые изучаются по другим программам. Чем наш учебник хуже? Включим какие-нибудь дополнительные главы. Школьники не знают правило деления уголком? Это же элементарная математика. Надо сделать такой параграф необязательным, озаглавив его «для тех, кто хочет знать больше». Репетиторы против? А какое нам дело до репетиторов вообще? Методисты и преподаватели школ тоже против? Мы не будем усложнять материал и рассмотрим наиболее простую его часть.
И вот тут начинается. Простота темы и качество ее усвоения заключатся, прежде всего, в понимании ее логики, а не в том, чтобы согласно предписанию авторов учебника выполнить некий набор не понятно как связанных друг с другом операций. Иначе туман в голове школьника будет обеспечен. Если расчет авторов идет на относительно сильных учеников (но обучающихся по обычной программе), то не стоит подавать тему в командной форме. А что мы видим в учебнике? Дети, надо делить по такому правилу. Получите многочлен под уголком. Таким образом, первоначальный многочлен разложится на множители. Однако, понять, почему именно так подбираются слагаемые под уголком, почему их надо умножать на многочлен над уголком, а затем вычитать из текущего остатка — непонятно. И самое главное не понятно, почему подобранные одночлены надо в итоге сложить и почему получившиеся скобки будут разложением первоначального многочлена. Любой грамотный математик поставит жирный знак вопроса над теми объяснениями, которые даются в учебнике.
Я предлагаю вниманию репетиторов и преподавателей математики свое решение проблемы, которое практически делает для ученика очевидным все то, что изложено в учебнике. Фактически мы докажем теорему Безу: если число а — корень многочлена, то этот многочлен можно разложить на множители, один из который x-a, а второй получается из первоначального одним из трех способов: выделением линейного множителя через преобразования, делением уголком или по схеме Горнера. Именно с такой форомулировкой репетитору по математике будет легче работать.
Что такое методика преподавания? Прежде всего это четкий порядок в последовательности объяснений и примеров, на основе которых делаются математические выводы. Данная тема не исключение. Репетитору по математике очень важно познакомить ребенка с теоремой Безу до того, как будет выполняться деление уголком. Это очень важно! Добиться понимания лучше всего на конкретном примере. Возьмем какой-нибдуь многочлен с подобранным корнем и показажем технику его разложения на множители при помощи знакомого школьнику еще с 7 класса метода тождественных преобразований. При соответствующих сопроводительных пояснениях, акцентах и подсказках репетитора по математике вполне реально донести материал без каких-либо общих математических выкладок, произвольных коэффициентов и степеней.
Важный совет репетитору по математике — следовать инструкциям от начала и до конца и не менять эту последовательнотсь.
Итак, допустим, что перед нами многочлен  . Если мы подставим вместо его икса число 1, то значение многочлена будет равно нулю. Следовательно х=1 — его корень. Попробуем разложить
. Если мы подставим вместо его икса число 1, то значение многочлена будет равно нулю. Следовательно х=1 — его корень. Попробуем разложить  на два слагаемых так, чтобы одно из них было произведением линейного выражения
на два слагаемых так, чтобы одно из них было произведением линейного выражения  и некоторого одночлена, а второе имело бы степень на единицу меньше, чем
и некоторого одночлена, а второе имело бы степень на единицу меньше, чем  . То есть представим его в виде
. То есть представим его в виде
 . Если мы подставим вместо его икса число 1, то значение многочлена будет равно нулю. Следовательно х=1 — его корень. Попробуем разложить
. Если мы подставим вместо его икса число 1, то значение многочлена будет равно нулю. Следовательно х=1 — его корень. Попробуем разложить  на два слагаемых так, чтобы одно из них было произведением линейного выражения
на два слагаемых так, чтобы одно из них было произведением линейного выражения  и некоторого одночлена, а второе имело бы степень на единицу меньше, чем
и некоторого одночлена, а второе имело бы степень на единицу меньше, чем  . То есть представим его в виде
. То есть представим его в видеОдночлен для красного поля подберем так, чтобы при при умножении его на
 старший член полностью совпадал со старшим членом первоначального многочлена. Если ученик не самый слабый, то он вполне способен будет назвать репетитору по математике искомое выражение:
старший член полностью совпадал со старшим членом первоначального многочлена. Если ученик не самый слабый, то он вполне способен будет назвать репетитору по математике искомое выражение:  . Репетитору следует тут же предложить вставить его в красное поле и показать что будет получаться при их раскрытии. Лучше всего этот виртуальный временный многочлен подписать под стрелочками (под фотанчиком), выделяя его каким-нибудь цветом, например, синим. Это поможет подоборать слагаемое для красного поля, называемое остатком от выделения. Я бы советовал репетиторам именно здесь указывать на то, что этот остаток можно находить вычитанием. Выполняя такую операцию получим:
. Репетитору следует тут же предложить вставить его в красное поле и показать что будет получаться при их раскрытии. Лучше всего этот виртуальный временный многочлен подписать под стрелочками (под фотанчиком), выделяя его каким-нибудь цветом, например, синим. Это поможет подоборать слагаемое для красного поля, называемое остатком от выделения. Я бы советовал репетиторам именно здесь указывать на то, что этот остаток можно находить вычитанием. Выполняя такую операцию получим:
Репетитор по математике должен обратить внимание ученика на то, что подставляя единицу в данное равенство, мы гарантировано получим нуль в его левой части (так как 1 — корень первоначального многочлена), а в правой, очевидно, тоже обнулим первое слагаемое. Значит без всякой проверки можно сказать, что единица — корень «зеленого остатка».
Поступим с ним так же, как мы это сделали с первоначальным многочленом, выделяя из него такой же линейный множитель  . Репетитор по математике рисует перед учеником две рамки и просит заполнить слева направо.
. Репетитор по математике рисует перед учеником две рамки и просит заполнить слева направо.
 . Репетитор по математике рисует перед учеником две рамки и просит заполнить слева направо.
. Репетитор по математике рисует перед учеником две рамки и просит заполнить слева направо.
Ученик подбирает репетитору одночлен для красного поля так, чтобы он при умножении на старшее слагаемое линейного выражения давал старшее слагаемое раскладывающегося многочлена. Вписываем
давал старшее слагаемое раскладывающегося многочлена. Вписываем  в касную рамку, тут же раскрываем скобку и выделяем синим цветом то выражение, которое надо вычесть их раскладывающегося. Выполняя эту операцию получаем
в касную рамку, тут же раскрываем скобку и выделяем синим цветом то выражение, которое надо вычесть их раскладывающегося. Выполняя эту операцию получаем
 давал старшее слагаемое раскладывающегося многочлена. Вписываем
давал старшее слагаемое раскладывающегося многочлена. Вписываем  в касную рамку, тут же раскрываем скобку и выделяем синим цветом то выражение, которое надо вычесть их раскладывающегося. Выполняя эту операцию получаем
в касную рамку, тут же раскрываем скобку и выделяем синим цветом то выражение, которое надо вычесть их раскладывающегося. Выполняя эту операцию получаем
И, наконец, проделывая тоже самое с последним остатком 


получим окончательно

Теперь вынесем выражение  за скобку и перед нами окажется разложение первоначального многочлена на множители один из которых «икс минус подобранный корень».
за скобку и перед нами окажется разложение первоначального многочлена на множители один из которых «икс минус подобранный корень».
 за скобку и перед нами окажется разложение первоначального многочлена на множители один из которых «икс минус подобранный корень».
за скобку и перед нами окажется разложение первоначального многочлена на множители один из которых «икс минус подобранный корень».
Для того, чтобы ученику не казалось, что последний «зеленый остаток» случайно разложился на нужные множители, репетитор по математкие должен указать на важное свойство всех зеленых остатков — каждый из них имеет корень 1. Поскольку степени этих остатков убывают, то какая бы степень начального многочлена ни была нам дана, рано или поздно, мы получим линейный «зеленый остаток» с корнем 1, а следовательно он обязательно разложиться на произведение некоторого числа и выражения  .
.
 .
.
После такой подготовительной работы репетитору по математкие не составит труда объяснить ученику, что происходит при делении уголком. Это тот же самый процесс, только в более краткой и компактной форме, без знаков равно и без переписываний одних и тех же выделенных слагаемых. Многочлен из которого выделяется линейный множитель записываем слева от уголка, подбираемые красные одночлены собираем под уголом (теперь становится понятно, почему они должны складываться), для получения «синих многочленов» надо «красные» умножать на x-1, а затем вычитать из текущего выделяемого как это делается при обычном делении чисел в столбик (вот она аналогия с раннее изученным). Получаемые «зеленые остатки» подвергаются новому выделению и подбору «красных одночленов» . И так до получения нулевого «зеленого остатка». Самое главное, что ученику становится понятна дальнейшая судьба записанных многочленов над и под уголком. Очевидно, это скобки, произведение которых равно первоначальному многочлену.
Следующий этап работы репетитора по математике — формулирование теоремы Безу. Cобственно ее формулировка при таком подходе репетитора становится очевидной: если число а — корень многочлена, то его можно разложить на множители, один из которых  , а другой получается из первоначального одним из трех способов:
, а другой получается из первоначального одним из трех способов:
 , а другой получается из первоначального одним из трех способов:
, а другой получается из первоначального одним из трех способов:- непосредственным разложением (аналогом метода группировки)
- делением уголком (в столбик)
- через схему Горнера
Надо сказать, что схему горнера показывают ученикам далеко не все репетиторы математики и не все школьные преподаватели (к счастью для самих репетиторов) заходят на уроках так глубоко в тему. Однако, для учащегося математического класса я не вижу никаких оснований для остановки на делении в столбик. Более того, самый удобный и быстрый прием разложения основан именно на схеме Горнера. Для того, чтобы объяснить ребенку откуда она берется достаточно проследить на примере деления уголком появление старших коэффициентов у зеленых остатках. Становится ясно, что старший коэффициент начального многочлена сносится в коэффициент первого «красного одночлена», а дальше от второго коэффициента текущего верхнего многочлена вычитается результат умножения текущего коэффициента «красного одночлена» на  . Поэтому можно прибавлять результат умножения на
. Поэтому можно прибавлять результат умножения на  . После акцентирования внимания ученика на специфике действий с коэффициентами репетитор по математике может показать как обычно эти действия выполняют без записи самих переменных. Для этого удобно корень
. После акцентирования внимания ученика на специфике действий с коэффициентами репетитор по математике может показать как обычно эти действия выполняют без записи самих переменных. Для этого удобно корень  и коэффициенты первоначального многочлена по старшинству занести в такую таблицу:
и коэффициенты первоначального многочлена по старшинству занести в такую таблицу:
 . Поэтому можно прибавлять результат умножения на
. Поэтому можно прибавлять результат умножения на  . После акцентирования внимания ученика на специфике действий с коэффициентами репетитор по математике может показать как обычно эти действия выполняют без записи самих переменных. Для этого удобно корень
. После акцентирования внимания ученика на специфике действий с коэффициентами репетитор по математике может показать как обычно эти действия выполняют без записи самих переменных. Для этого удобно корень  и коэффициенты первоначального многочлена по старшинству занести в такую таблицу:
и коэффициенты первоначального многочлена по старшинству занести в такую таблицу:
Если в многочлене пропущена какая-нибудь степень, то в таблицу принудительно вносится ее нулевой коэффициент. В нижнюю строчку поочередно вписываются коэффициенты «красных многочленов» по правилу «крючка»:


Корень умножается на последний снесенный «красный коэффициент», прибавляется к следующему коэффициенту верхней строки и результат сносится в нижнюю строчку . В последней колонке гарантированно получим старший коэффициент последнего «зеленого остатка», то есть нуль. После завершения процесса, числа, зажатые между подобранным корнем и нулевым остатком оказываются коэффициентами второго (нелинейного) множителя.

Поскольку корень а дает в конце нижней строки нуль, то схему Горнера можно использовать для проверки чисел на звание корень многочлена. Если специальная теорема о подборе рационального корня. Все кандидаты на это звание, полученные с ее помощью, просто вставляются по очереди слева в схему Горнера. Как только мы получим нуль, тестируемое число будет корнем, и одновременно в его строчке получим коэффициенты разложения первоначального многочлена на множители. Очень удобно.
В завершение хотелось бы отметить, что для аккуратного введения схемы Горнера , а также для практического закрепления темы, репетитор по математике должен иметь в своем распоряжении достаточное количество часов. Репетитору, работающему с режимом «раз в неделю» не стоит заниматься делением уголком. На Егэ по математике и на ГИА по математике вряд ли в первой части когда-нибудь встретится уравнение третьей степени, решаемое такими средствами. Если репетитор готовит ребенка экзамену по математике в МГУ — изучение темы становится обязательным. Очень уж любят преподаватели ВУЗов, не в пример составителям ЕГЭ, проверить глубину знаний абитуриента.
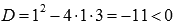 , то есть, действительных корней трехчлен не имеет, но имеет пару комплексно сопряженных
, то есть, действительных корней трехчлен не имеет, но имеет пару комплексно сопряженных 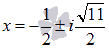 .
.
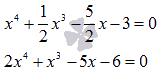
Решение уравнений высших степеней.
В общем случае уравнение степени выше четвертой не разрешимо в радикалах. Однако, иногда можно отыскать корни многочлена, который находится в левой части уравнения высшей степени, представив его в виде призведения многочленов степени не выше четвертой. Таким образом, разложение многочлена на множители лежит в основе решения таких уравнений, поэтому, рекомендуем подробно изучить этот раздел, прежде чем двигаться дальше.
Достаточно часто рассматриваются уравнения высших степеней с целыми коэффициентами. В этом случае можно попытаться найти рациональные корни уравнения, после чего можно разложить на множители многочлен, находящийся в левой части исходного уравнения, тем самым перейти к нахождению корней уравнения, степень которого будет ниже.
В этой статье как раз разберемся с решением уравнений высших степеней с целыми коэффициентами.
Уравнения высших степеней с целыми коэффициентами.
Любое уравнение вида 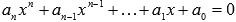 можно свести к приведенному уравнению той же степени домножив обе его части на
можно свести к приведенному уравнению той же степени домножив обе его части на 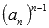 и выполнив замену переменной вида
и выполнив замену переменной вида 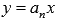 :
:
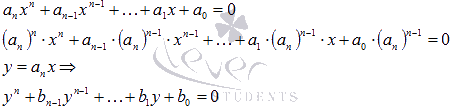
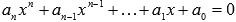 можно свести к приведенному уравнению той же степени домножив обе его части на
можно свести к приведенному уравнению той же степени домножив обе его части на 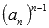 и выполнив замену переменной вида
и выполнив замену переменной вида 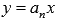 :
: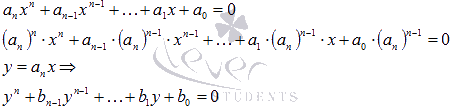
Полученные коэффициенты 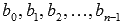 тоже будут целыми.
тоже будут целыми.
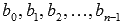 тоже будут целыми.
тоже будут целыми.
Таким образом, будем решать приведенное уравнение степени n с целыми коэффициентами вида  .
.
 .
.
Алгоритм решения.
- Находим целые корни уравнения.Целые корни уравнения
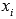 , i=1, 2, …, m (m – количество целых корней уравнения) находятся среди делителей свободного члена
, i=1, 2, …, m (m – количество целых корней уравнения) находятся среди делителей свободного члена 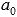 . То есть, первым делом выписываем делители свободного члена и подставляем их по очереди в исходное равенство для проверки. Перебираем их по очереди, пока не получим тождество. Как только тождество получено, то первый целый корень уравнения найден и уравнение предстает в виде
. То есть, первым делом выписываем делители свободного члена и подставляем их по очереди в исходное равенство для проверки. Перебираем их по очереди, пока не получим тождество. Как только тождество получено, то первый целый корень уравнения найден и уравнение предстает в виде 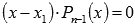 , где
, где 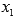 - корень уравнения, а
- корень уравнения, а 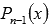 - частное от деления
- частное от деления 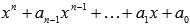 на
на 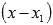 .Продолжаем подставлять выписанные ранее делители в уравнение
.Продолжаем подставлять выписанные ранее делители в уравнение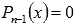 , начиная с
, начиная с 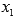 (так как корни могут повторяться). Как только получаем тождество, то корень
(так как корни могут повторяться). Как только получаем тождество, то корень 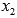 найден и уравнение предстает в виде
найден и уравнение предстает в виде 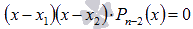 , где
, где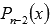 - частное от деления
- частное от деления 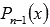 на
на 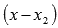 .И так продолжаем перебор делителей, начиная с
.И так продолжаем перебор делителей, начиная с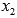 . В итоге найдем все m целых корней уравнения и оно представится в виде
. В итоге найдем все m целых корней уравнения и оно представится в виде 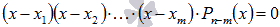 , где
, где 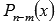 - многочлен степени n-m. Весь этот процесс удобно проводить по схеме Горнера.Дробных корней приведенное уравнение с целыми коэффициентами иметь не может.
- многочлен степени n-m. Весь этот процесс удобно проводить по схеме Горнера.Дробных корней приведенное уравнение с целыми коэффициентами иметь не может. - Находим оставшиеся корни (иррациональные и/или комплексные) из уравнения
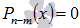 любым способом.
любым способом.
Разберем алгоритм на примере.
Пример.
Решить уравнение 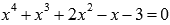 .
.
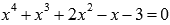 .
.
Решение.
Во-первых, найдем все целые корни данного уравнения.
Свободным членом является -3. Его делителями являются числа 1, -1, 3 и -3.
Будем подставлять их по очереди в исходное равенство до получения тождества.
При х=1 имеем 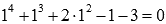 . То есть х=1 является корнем уравнения.
. То есть х=1 является корнем уравнения.
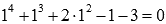 . То есть х=1 является корнем уравнения.
. То есть х=1 является корнем уравнения.
Разделим многочлен 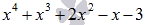 на (х-1) столбиком:
на (х-1) столбиком:
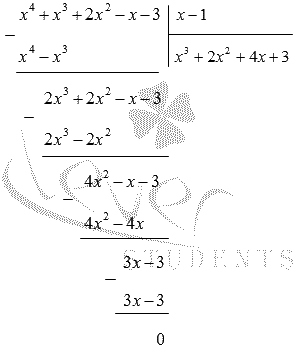
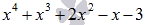 на (х-1) столбиком:
на (х-1) столбиком: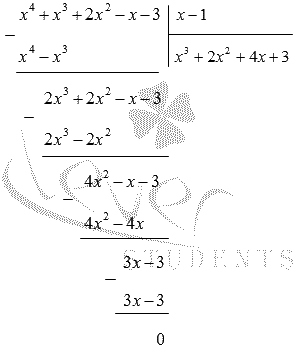
Следовательно, 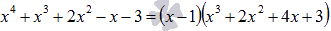 .
.
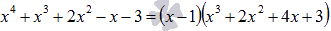 .
.
Продолжим перебор делителей, но уже для равенства 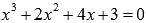 :
:
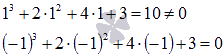
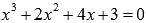 :
: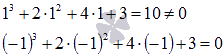
При х = -1 получили верное равенство, следовательно, -1 является корнем уравнения.
Разделим 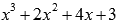 на (х+1) столбиком:
на (х+1) столбиком:
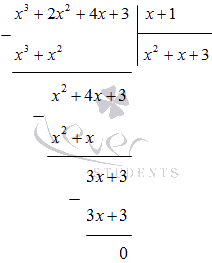
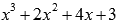 на (х+1) столбиком:
на (х+1) столбиком: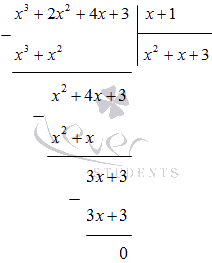
Таким образом,
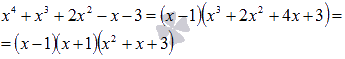
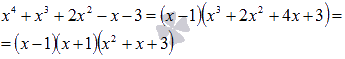
Продолжаем перебор делителей для равенства 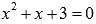 , начиная с х = -1:
, начиная с х = -1:
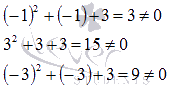
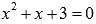 , начиная с х = -1:
, начиная с х = -1: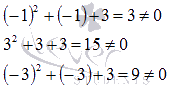
Получили неверные равенства, следовательно, целых корней уравнение больше не имеет.
Оставшиеся корни исходного уравнения являются корнями квадратного трехчлена 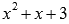 .
.
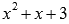 .
.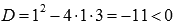 , то есть, действительных корней трехчлен не имеет, но имеет пару комплексно сопряженных
, то есть, действительных корней трехчлен не имеет, но имеет пару комплексно сопряженных 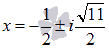 .
.
Замечание.
Можно было использовать схему Горнера вместо деления многочленов столбиком.
Решение было бы следующим.
Как только выяснили, что x=1 является корнем уравнения, то имеем


Таблица коэффициентов схемы Горнера сразу дает коэффициенты частного от деления многочленов, то есть 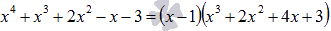 .
.
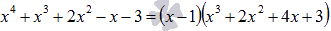 .
.
Как только выясняем, что х = -1 является следующим решением уравнения, то по схеме Горнера имеем


После этого шага метода Горнера приходим к разложению 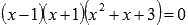 . После проверки оставшихся делителей для равенства
. После проверки оставшихся делителей для равенства 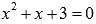 переходим к нахождению оставшихся корней.
переходим к нахождению оставшихся корней.
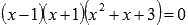 . После проверки оставшихся делителей для равенства
. После проверки оставшихся делителей для равенства 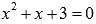 переходим к нахождению оставшихся корней.
переходим к нахождению оставшихся корней.
Ответ:
х = -1, х=1, 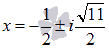 .
.
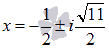 .
.
Пример.
Найти корни уравнения 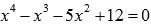 .
.
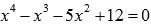 .
.
Решение.
Делителями свободного члена являются числа 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 12 и -12.
Проводим проверку:
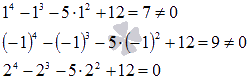
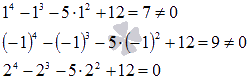
То есть, х=2 является корнем уравнения. Делим 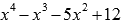 на х-2 по схеме Горнера:
на х-2 по схеме Горнера:
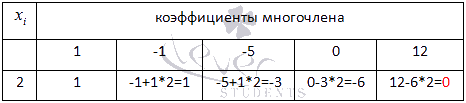
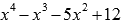 на х-2 по схеме Горнера:
на х-2 по схеме Горнера:
Получаем 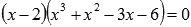 .
.
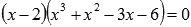 .
.
Продолжаем проверку делителей для равенства 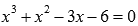 , начиная с х=2.
, начиная с х=2.
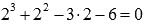
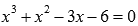 , начиная с х=2.
, начиная с х=2.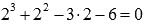
То есть, х=2 опять является корнем. Делим 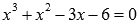 на х-2
на х-2

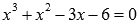 на х-2
на х-2
Получаем 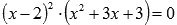 .
.
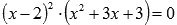 .
.
Проверять оставшиеся делители для равенства 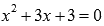 нет смысла, так как быстрее найти корни этого квадратного трехчлена через дискриминант.
нет смысла, так как быстрее найти корни этого квадратного трехчлена через дискриминант.
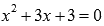 нет смысла, так как быстрее найти корни этого квадратного трехчлена через дискриминант.
нет смысла, так как быстрее найти корни этого квадратного трехчлена через дискриминант.
Решаем квадратное уравнение:
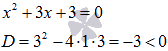 .
.
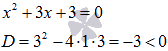 .
.
Следовательно, корнями является комплексно сопряженная пара 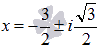 .
.
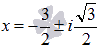 .
.
Ответ:
х=2, 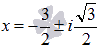 .
.
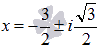 .
.
Пример.
Найти действительные корни уравнения 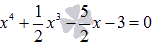 .
.
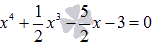 .
.
Решение.
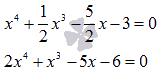
Домножим на 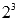 обе части уравнения:
обе части уравнения:
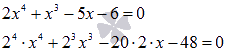
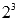 обе части уравнения:
обе части уравнения: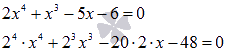
Проведем замену переменных y = 2x:
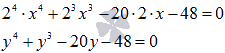
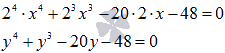
Пришли к приведенному уравнению четвертой степени. Решаем его по стандартному алгоритму: проверяем делители, проводим деление и в результате выясняем, что уравнение имеет два действительных корня y = -2, y=3 и два комплексных (решение не приводим).
В силу замены, действительными корнями исходного уравнения являются 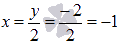 и
и 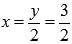 .
.
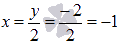 и
и 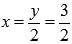 .
.
Смотрите также статьи решение кубических уравнений и решение уравнений четвертой степени.
Схема Горнера.
Для вычисления коэффициентов частного и остатка от деления многочлена  на линейный двучлен x-s очень удобно использоватьсхему Горнера (иногда называют метод Горнера).
на линейный двучлен x-s очень удобно использоватьсхему Горнера (иногда называют метод Горнера).
 на линейный двучлен x-s очень удобно использоватьсхему Горнера (иногда называют метод Горнера).
на линейный двучлен x-s очень удобно использоватьсхему Горнера (иногда называют метод Горнера).
Заполняется таблица:


Полученные числа  являются коэффициентами частного от деления многочлена
являются коэффициентами частного от деления многочлена  на двучлен x-s, а
на двучлен x-s, а  - остатком. То есть,
- остатком. То есть,

 являются коэффициентами частного от деления многочлена
являются коэффициентами частного от деления многочлена  на двучлен x-s, а
на двучлен x-s, а  - остатком. То есть,
- остатком. То есть,
Пример.
Найти частное и остаток от деления многочлена  на линейный двучлен х-1.
на линейный двучлен х-1.
 на линейный двучлен х-1.
на линейный двучлен х-1.
Решение.
В нашем примере s = 1, коэффициенты  .
.
 .
.
Воспользуемся схемой Горнера:


Таким образом,  - частное,
- частное,  - остаток от деления.
- остаток от деления.
 - частное,
- частное,  - остаток от деления.
- остаток от деления.
В следующем примере не будем давать такие подробные пояснения.
Пример.
Убедиться, что многочлен  делится на двучлен
делится на двучлен  без остатка и найти частное.
без остатка и найти частное.
 делится на двучлен
делится на двучлен  без остатка и найти частное.
без остатка и найти частное.
Решение.
Проверим это с использованием схемы Горнера:


Получили остаток равный нулю, что говорит о делимости исходного многочлена без остатка на двучлен. Частным является многочлен 

Когда  , то можно говорить о делимости многочлена
, то можно говорить о делимости многочлена  на двучлен x-s, другими словами, s – корень исходного многочлена. По следствию из теоремы Безу, такой многочлен представляется в виде произведения:
на двучлен x-s, другими словами, s – корень исходного многочлена. По следствию из теоремы Безу, такой многочлен представляется в виде произведения:

 , то можно говорить о делимости многочлена
, то можно говорить о делимости многочлена  на двучлен x-s, другими словами, s – корень исходного многочлена. По следствию из теоремы Безу, такой многочлен представляется в виде произведения:
на двучлен x-s, другими словами, s – корень исходного многочлена. По следствию из теоремы Безу, такой многочлен представляется в виде произведения:
Поэтому, схему Горнера удобно применять для отыскания целых корней приведенныхуравнений высших степеней с целыми коэффициентами и для разложения многочленов на множители.
Пример.
Найти корни уравнения  и разложить многочлен в левой части уравнения на множители.
и разложить многочлен в левой части уравнения на множители.
 и разложить многочлен в левой части уравнения на множители.
и разложить многочлен в левой части уравнения на множители.
Решение.
Если это уравнение имеет целые корни, то они находятся среди делителей свободного члена. Запишем эти делители 1,-1,2,-2,3,-3,6,-6.
Проверим их по схеме Горнера.


То есть, х=1 корнем не является.
Продолжаем схему Горнера.


То есть, х=-1 является корнем, и исходный многочлен представится в виде 

Продолжим проверку делителей, начиная с х=-1 (так как корни могут повторяться), но в схеме Горнера коэффициентами будем считать значения последней полученной строки:


То есть, х=-1 не является повторяющимся (кратным) корнем. Проверяем следующий делитель:


То есть, х=2 не является корнем. Продолжаем схему Горнера для х=-2:


То есть, х=-2 является корнем уравнения, многочлен представляется в виде


Таким образом, получили требуемое разложение. Из него видно, что последним третьим корнем является х=3. Завершим таблицу, в качестве коэффициентов будем использовать уже значения последней полученной строки:


Вывод: последняя таблица, заполненная по схеме Горнера, по сути, является решением рассмотренного примера.
Конечно, можно было схему Горнера заменить делением многочлена на линейный двучлен столбиком. Но о вкусах, как известно, не спорят.
Ответ:
х=-1, х=-2, х=3,  .
.
 .
.
Комментариев нет:
Отправить комментарий