Знание основных элементарных функций, их свойств и графиков не менее важно, чем знание таблицы умножения. Они как фундамент, на них все основано, из них все строится и к ним все сводится.
Здесь мы перечислим все основные элементарные функции, приведем их графики и дадим без вывода и доказательств свойства основных элементарных функций по схеме:
- область определения функции;
- поведение функции на границах области определения, вертикальные асимптоты (при необходимости смотрите статью классификация точек разрыва функции);
- четность и нечетность;
- область значений функции;
- промежутки возрастания и убывания, точки экстремума;
- промежутки выпуклости (выпуклости вверх) и вогнутости (выпуклости вниз), точки перегиба (при необходимости смотрите статью выпуклость функции, направление выпуклости, точки перегиба, условия выпуклости и перегиба);
- наклонные и горизонтальные асимптоты;
- особые точки функций;
- особые свойства некоторых функций (например, наименьший положительный период у тригонометрических функций).
Если Вас интересует дифференцирование элементарных функций или интегрирование элементарных функций, то можете перейти к этим разделам теории.
Основными элементарными функциями являются: постоянная функция (константа), кореньn-ой степени, степенная функция, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции.
Постоянная функция.
Постоянная функция задается на множестве всех действительных чисел формулой 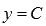 , гдеC – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.
, гдеC – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.
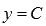 , гдеC – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.
, гдеC – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.
Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,C). Для примера покажем графики постоянных функций y=5,y=-2 и 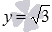 , которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.
, которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.
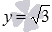 , которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.
, которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.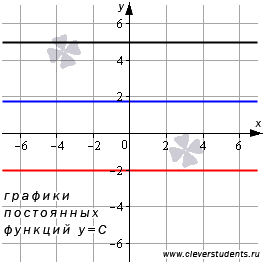
Свойства постоянной функции.
- Область определения: все множество действительных чисел.
- Постоянная функция является четной.
- Область значений: множество, состоящее из единственного числа С.
- Постоянная функция невозрастающая и неубывающая (на то она и постоянная).
- Говорить о выпуклости и вогнутости постоянной не имеет смысла.
- Асимптот нет.
- Функция проходит через точку (0,C) координатной плоскости.
Корень n-ой степени.
Рассмотрим основную элементарную функцию, которая задается формулой 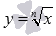 , где n – натуральное число, большее единицы.
, где n – натуральное число, большее единицы.
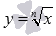 , где n – натуральное число, большее единицы.
, где n – натуральное число, большее единицы.Корень n-ой степени, n - четное число.
Начнем с функции корень n-ой степени при четных значениях показателя корня n.
Для примера приведем рисунок с изображениями графиков функций 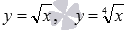 и
и 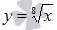 , им соответствуют черная, красная и синяя линии.
, им соответствуют черная, красная и синяя линии.
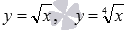 и
и 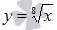 , им соответствуют черная, красная и синяя линии.
, им соответствуют черная, красная и синяя линии.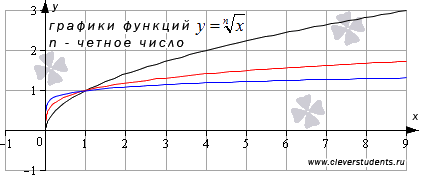
Аналогичный вид имеют графики функций корень четной степени при других значениях показателя.
Свойства функции корень n-ой степени при четных n.
- Область определения: множество всех неотрицательных действительных чисел
 .
. - При x=0 функция
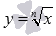 принимает значение, равное нулю.
принимает значение, равное нулю. - Эта функция общего вида (не является четной или нечетной).
- Область значений функции:
 .
. - Функция
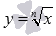 при четных показателях корня возрастает на всей области определения.
при четных показателях корня возрастает на всей области определения. - Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.
- Асимптот нет.
- График функции корень n-ой степени при четных n проходит через точки (0,0) и(1,1).
Корень n-ой степени, n - нечетное число.
Функция корень n-ой степени с нечетным показателем корня n определена на всем множестве действительных чисел. Для примера приведем графики функций 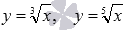 и
и 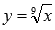 , им соответствуют черная, красная и синяя кривые.
, им соответствуют черная, красная и синяя кривые.
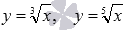 и
и 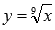 , им соответствуют черная, красная и синяя кривые.
, им соответствуют черная, красная и синяя кривые.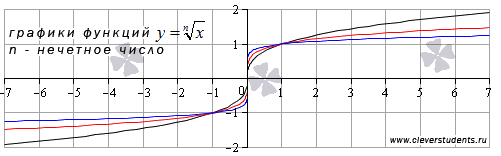
При других нечетных значениях показателя корня графики функции 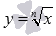 будут иметь схожий вид.
будут иметь схожий вид.
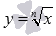 будут иметь схожий вид.
будут иметь схожий вид.
Свойства функции корень n-ой степени при нечетных n.
- Область определения: множество всех действительных чисел.
- Эта функция нечетная.
- Область значений функции: множество всех действительных чисел.
- Функция
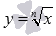 при нечетных показателях корня возрастает на всей области определения.
при нечетных показателях корня возрастает на всей области определения. - Эта функция вогнутая на промежутке
 и выпуклая на промежутке
и выпуклая на промежутке  , точка с координатами (0,0) – точка перегиба.
, точка с координатами (0,0) – точка перегиба. - Асимптот нет.
- График функции корень n-ой степени при нечетных n проходит через точки (-1,-1),(0,0) и (1,1).
Степенная функция.
Степенная функция задается формулой вида  .
.
 .
.
Рассмотрим вид графиков степенной функции и свойства степенной функции в зависимости от значения показателя степени.
Начнем со степенной функции с целым показателем a. В этом случае вид графиков степенных функций и свойства функций зависят от четности или нечетности показателя степени, а также от его знака. Поэтому сначала рассмотрим степенные функции  при нечетных положительных значениях показателя a, далее - при четных положительных, далее - при нечетных отрицательных показателях степени, и, наконец, при четных отрицательных a.
при нечетных положительных значениях показателя a, далее - при четных положительных, далее - при нечетных отрицательных показателях степени, и, наконец, при четных отрицательных a.
 при нечетных положительных значениях показателя a, далее - при четных положительных, далее - при нечетных отрицательных показателях степени, и, наконец, при четных отрицательных a.
при нечетных положительных значениях показателя a, далее - при четных положительных, далее - при нечетных отрицательных показателях степени, и, наконец, при четных отрицательных a.
Свойства степенных функций с дробными и иррациональными показателями (как и вид графиков таких степенных функций) зависят от значения показателя a. Их будем рассматривать, во-первых, при a от нуля до единицы, во-вторых, при a больших единицы, в-третьих, при a от минус единицы до нуля, в-четвертых, при a меньших минус единицы.
В заключении этого пункта для полноты картины опишем степенную функцию с нулевым показателем.
Степенная функция с нечетным положительным показателем.
Рассмотрим степенную функцию  при нечетном положительном показателе степени, то есть, при а=1,3,5,….
при нечетном положительном показателе степени, то есть, при а=1,3,5,….
 при нечетном положительном показателе степени, то есть, при а=1,3,5,….
при нечетном положительном показателе степени, то есть, при а=1,3,5,….
На рисунке ниже приведены графики степенных фнукций 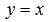 – черная линия,
– черная линия, 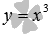 – синяя линия,
– синяя линия, 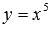 – красная линия,
– красная линия, 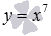 – зеленая линия. При а=1 имеем линейную функцию y=x.
– зеленая линия. При а=1 имеем линейную функцию y=x.
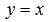 – черная линия,
– черная линия, 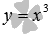 – синяя линия,
– синяя линия, 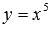 – красная линия,
– красная линия, 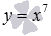 – зеленая линия. При а=1 имеем линейную функцию y=x.
– зеленая линия. При а=1 имеем линейную функцию y=x.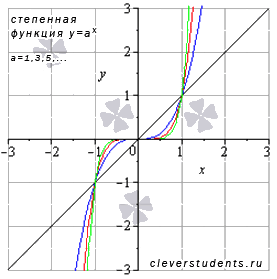
Свойства степенной функции с нечетным положительным показателем.
- Область определения:
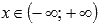 .
. - Область значений:
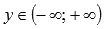 .
. - Функция нечетная, так как
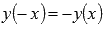 .
. - Функция возрастает при
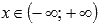 .
. - Функция выпуклая при
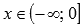 и вогнутая при
и вогнутая при 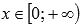 (кроме линейной функции).
(кроме линейной функции). - Точка (0;0) является точкой перегиба (кроме линейной функции).
- Асимптот нет.
- Функция проходит через точки (-1;-1), (0;0), (1;1).
Степенная функция с четным положительным показателем.
Рассмотрим степенную функцию  с четным положительным показателем степени, то есть, при а=2,4,6,….
с четным положительным показателем степени, то есть, при а=2,4,6,….
 с четным положительным показателем степени, то есть, при а=2,4,6,….
с четным положительным показателем степени, то есть, при а=2,4,6,….
В качестве примера приведем графики степенных функций 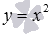 – черная линия,
– черная линия, 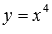 – синяя линия,
– синяя линия, 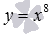 – красная линия. При а=2 имеем квадратичную функцию, графиком которой является квадратичная парабола.
– красная линия. При а=2 имеем квадратичную функцию, графиком которой является квадратичная парабола.
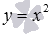 – черная линия,
– черная линия, 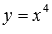 – синяя линия,
– синяя линия, 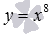 – красная линия. При а=2 имеем квадратичную функцию, графиком которой является квадратичная парабола.
– красная линия. При а=2 имеем квадратичную функцию, графиком которой является квадратичная парабола.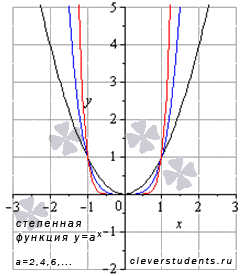
Свойства степенной функции с четным положительным показателем.
- Область определения:
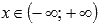 .
. - Область значений:
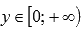 .
. - Функция четная, так как
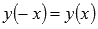 .
. - Функция возрастает при
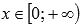 , убывает при
, убывает при 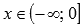 .
. - Функция вогнутая при
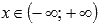 .
. - Точек перегиба нет.
- Асимптот нет.
- Функция проходит через точки (-1;1), (0;0), (1;1).
Степенная функция с нечетным отрицательным показателем.
Посмотрите на графики степенной функции  при нечетных отрицательных значениях показателя степени, то есть, при а=-1,-3,-5,….
при нечетных отрицательных значениях показателя степени, то есть, при а=-1,-3,-5,….
 при нечетных отрицательных значениях показателя степени, то есть, при а=-1,-3,-5,….
при нечетных отрицательных значениях показателя степени, то есть, при а=-1,-3,-5,….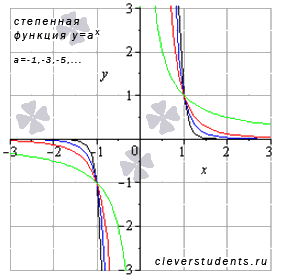
На рисунке в качестве примеров показаны графики степенных функций 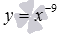 – черная линия,
– черная линия, 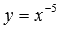 – синяя линия,
– синяя линия, 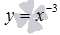 – красная линия,
– красная линия, 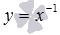 – зеленая линия. При а=-1имеем обратную пропорциональность, графиком которой является гипербола.
– зеленая линия. При а=-1имеем обратную пропорциональность, графиком которой является гипербола.
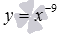 – черная линия,
– черная линия, 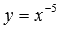 – синяя линия,
– синяя линия, 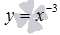 – красная линия,
– красная линия, 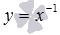 – зеленая линия. При а=-1имеем обратную пропорциональность, графиком которой является гипербола.
– зеленая линия. При а=-1имеем обратную пропорциональность, графиком которой является гипербола.
Свойства степенной функции с нечетным отрицательным показателем.
- Область определения:
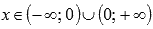 .
.
При x=0 имеем разрыв второго рода, так как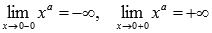 приа=-1,-3,-5,…. Следовательно, прямая x=0 является вертикальной асимптотой.
приа=-1,-3,-5,…. Следовательно, прямая x=0 является вертикальной асимптотой. - Область значений:
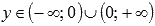 .
. - Функция нечетная, так как
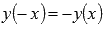 .
. - Функция убывает при
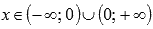 .
. - Функция выпуклая при
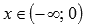 и вогнутая при
и вогнутая при  .
. - Точек перегиба нет.
- Горизонтальной асимптотой является прямая y = 0, так как
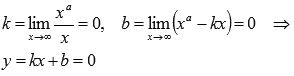
при а=-1,-3,-5,…. - Функция проходит через точки (-1;-1), (1;1).
Степенная функция с четным отрицательным показателем.
Перейдем к степенной функции  при а=-2,-4,-6,….
при а=-2,-4,-6,….
 при а=-2,-4,-6,….
при а=-2,-4,-6,….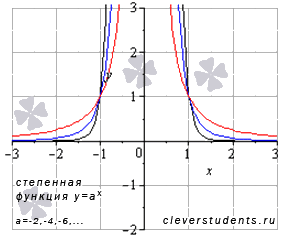
На рисунке изображены графики степенных функций 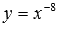 – черная линия,
– черная линия, 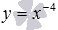 – синяя линия,
– синяя линия, 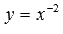 – красная линия.
– красная линия.
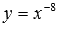 – черная линия,
– черная линия, 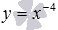 – синяя линия,
– синяя линия, 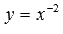 – красная линия.
– красная линия.
Свойства степенной функции с четным отрицательным показателем.
- Область определения:
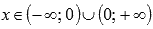 .
.
При x=0 имеем разрыв второго рода, так как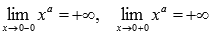 приа=-2,-4,-6,…. Следовательно, прямая x=0 является вертикальной асимптотой.
приа=-2,-4,-6,…. Следовательно, прямая x=0 является вертикальной асимптотой. - Область значений:
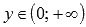 .
. - Функция четная, так как
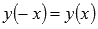 .
. - Функция возрастает при
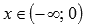 , убывает при
, убывает при  .
. - Функция вогнутая при
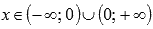 .
. - Точек перегиба нет.
- Горизонтальной асимптотой является прямая y=0, так как
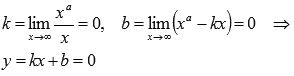
при а=-2,-4,-6,…. - Функция проходит через точки (-1;1), (1;1).
Степенная функция с рациональным или иррациональным показателем, значение которого больше нуля и меньше единицы.
Обратите внимание! Если a - положительная дробь с нечетным знаменателем, то некоторые авторы считают областью определения степенной функции интервал 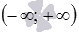 . При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными положительными показателями степени множество
. При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными положительными показателями степени множество 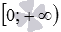 . Рекомендуем учащимся узнать взгляд Вашего преподавателя на этот тонкий момент, чтобы избежать разногласий.
. Рекомендуем учащимся узнать взгляд Вашего преподавателя на этот тонкий момент, чтобы избежать разногласий.
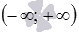 . При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными положительными показателями степени множество
. При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными положительными показателями степени множество 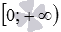 . Рекомендуем учащимся узнать взгляд Вашего преподавателя на этот тонкий момент, чтобы избежать разногласий.
. Рекомендуем учащимся узнать взгляд Вашего преподавателя на этот тонкий момент, чтобы избежать разногласий.
Рассмотрим степенную функцию  с рациональным или иррациональным показателем a, причем
с рациональным или иррациональным показателем a, причем 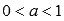 .
.
 с рациональным или иррациональным показателем a, причем
с рациональным или иррациональным показателем a, причем 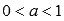 .
.
Приведем графики степенных функций  при а=11/12 (черная линия), а=5/7 (красная линия),
при а=11/12 (черная линия), а=5/7 (красная линия), 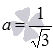 (синяя линия), а=2/5 (зеленая линия).
(синяя линия), а=2/5 (зеленая линия).
 при а=11/12 (черная линия), а=5/7 (красная линия),
при а=11/12 (черная линия), а=5/7 (красная линия), 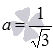 (синяя линия), а=2/5 (зеленая линия).
(синяя линия), а=2/5 (зеленая линия).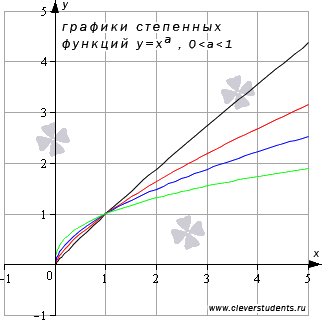
При других значениях показателя степени a, 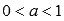 графики функции
графики функции  будут иметь схожий вид.
будут иметь схожий вид.
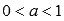 графики функции
графики функции  будут иметь схожий вид.
будут иметь схожий вид.
Свойства степенной функции при 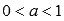 .
.
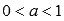 .
.- Область определения:
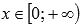 .
. - Область значений:
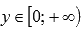 .
. - Функция не является ни четной, ни нечетной, то есть она общего вида.
- Функция возрастает при
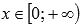 .
. - Функция выпуклая при
 .
. - Точек перегиба нет.
- Асимптот нет.
- Функция проходит через точки (0;0), (1;1).
Степенная функция с нецелым рациональным или иррациональным показателем, большим единицы.
Рассмотрим степенную функцию  с нецелым рациональным или иррациональным показателем a, причем
с нецелым рациональным или иррациональным показателем a, причем 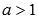 .
.
 с нецелым рациональным или иррациональным показателем a, причем
с нецелым рациональным или иррациональным показателем a, причем 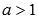 .
.
Приведем графики степенных функций, заданных формулами 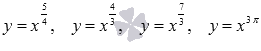 (черная, красная, синяя и зеленая линии соответственно).
(черная, красная, синяя и зеленая линии соответственно).
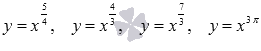 (черная, красная, синяя и зеленая линии соответственно).
(черная, красная, синяя и зеленая линии соответственно).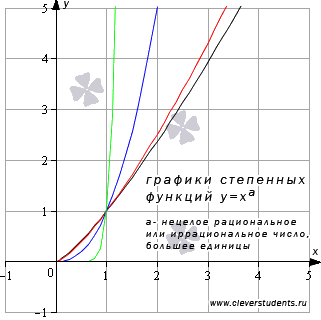
При других значениях показателя степени a, 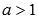 графики функции
графики функции  будут иметь схожий вид.
будут иметь схожий вид.
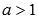 графики функции
графики функции  будут иметь схожий вид.
будут иметь схожий вид.
Свойства степенной функции при 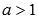 .
.
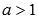 .
.- Область определения:
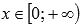 .
. - Область значений:
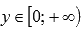 .
. - Функция не является ни четной, ни нечетной, то есть она общего вида.
- Функция возрастает при
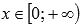 .
. - Функция вогнутая при
 , если
, если 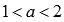 ; при
; при 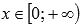 , если
, если 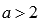 .
. - Точек перегиба нет.
- Асимптот нет.
- Функция проходит через точки (0;0), (1;1).
Степенная функция с действительным показателем, который больше минус единицы и меньше нуля.
Обратите внимание! Если a - отрицательная дробь с нечетным знаменателем, то некоторые авторы считают областью определения степенной функции интервал 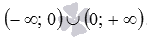 . При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными дробными отрицательными показателями степени множество
. При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными дробными отрицательными показателями степени множество 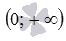 соответственно. Рекомендуем учащимся узнать взгляд Вашего преподавателя на этот тонкий момент, чтобы избежать разногласий.
соответственно. Рекомендуем учащимся узнать взгляд Вашего преподавателя на этот тонкий момент, чтобы избежать разногласий.
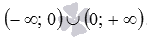 . При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными дробными отрицательными показателями степени множество
. При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными дробными отрицательными показателями степени множество 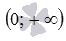 соответственно. Рекомендуем учащимся узнать взгляд Вашего преподавателя на этот тонкий момент, чтобы избежать разногласий.
соответственно. Рекомендуем учащимся узнать взгляд Вашего преподавателя на этот тонкий момент, чтобы избежать разногласий.
Переходим к степенной функции  , кгода
, кгода  .
.
 , кгода
, кгода  .
.
Чтобы хорошо представлять вид графиков степенных функций при  , приведем примеры графиков функций
, приведем примеры графиков функций 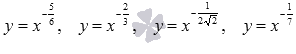 (черная, красная, синяя и зеленая кривые соответственно).
(черная, красная, синяя и зеленая кривые соответственно).
 , приведем примеры графиков функций
, приведем примеры графиков функций 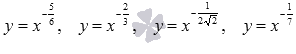 (черная, красная, синяя и зеленая кривые соответственно).
(черная, красная, синяя и зеленая кривые соответственно).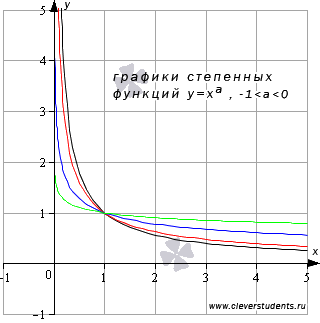
Свойства степенной функции с показателем a,  .
.
 .
.- Область определения:
 .
.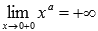 при
при 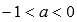 , следовательно, х=0 является вертикальной асимптотой.
, следовательно, х=0 является вертикальной асимптотой. - Область значений:
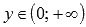 .
. - Функция не является ни четной, ни нечетной, то есть она общего вида.
- Функция убывает при
 .
. - Функция вогнутая при
 .
. - Точек перегиба нет.
- Горизонтальной асимптотой является прямая y=0.
- Функция проходит через точку (1;1).
Степенная функция с нецелым действительным показателем, который меньше минус единицы.
Приведем примеры графиков степенных функций  при
при 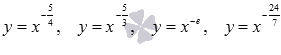 , они изображены черной, красной, синей и зеленой линиями соответственно.
, они изображены черной, красной, синей и зеленой линиями соответственно.
 при
при 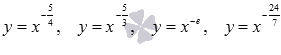 , они изображены черной, красной, синей и зеленой линиями соответственно.
, они изображены черной, красной, синей и зеленой линиями соответственно.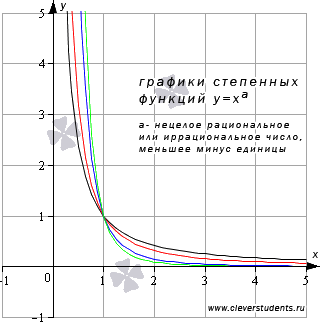
Свойства степенной функции с нецелым отрицательным показателем, меньшим минус единицы.
- Область определения:
 .
.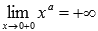 при
при 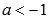 , следовательно, х=0 является вертикальной асимптотой.
, следовательно, х=0 является вертикальной асимптотой. - Область значений:
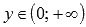 .
. - Функция не является ни четной, ни нечетной, то есть она общего вида.
- Функция убывает при
 .
. - Функция вогнутая при
 .
. - Точек перегиба нет.
- Горизонтальной асимптотой является прямая y=0.
- Функция проходит через точку (1;1).
При а=0 и 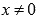 имеем функцию
имеем функцию 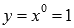 - это прямая из которой исключена точка (0;1)(выражению 00 условились не придавать никакого значения).
- это прямая из которой исключена точка (0;1)(выражению 00 условились не придавать никакого значения).
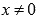 имеем функцию
имеем функцию 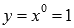 - это прямая из которой исключена точка (0;1)(выражению 00 условились не придавать никакого значения).
- это прямая из которой исключена точка (0;1)(выражению 00 условились не придавать никакого значения).Показательная функция.
Одной из основных элементарных функций является показательная функция.
График показательной функции 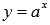 , где
, где 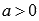 и
и 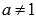 принимает различный вид в зависимости от значения основания а. Разберемся в этим.
принимает различный вид в зависимости от значения основания а. Разберемся в этим.
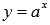 , где
, где 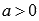 и
и 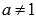 принимает различный вид в зависимости от значения основания а. Разберемся в этим.
принимает различный вид в зависимости от значения основания а. Разберемся в этим.
Сначала рассмотрим случай, когда основание показательной функции принимает значение от нуля до единицы, то есть, 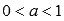 .
.
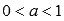 .
.
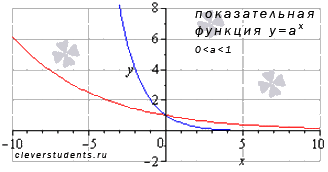
Для примера приведем графики показательной функции при а = 1/2 – синяя линия, a = 5/6 – красная линия. Аналогичный вид имеют графики показательной функции при других значениях основания из интервала 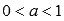 .
.
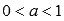 .
.
Свойства показательной функции с основанием меньшим единицы.
- Областью определения показательной функции является все множество действительнйх чисел:
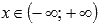 .
. - Область значений:
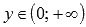 .
. - Функция не является ни четной, ни нечетной, то есть, она общего вида.
- Показательная функция, основание которой меньше единицы, убывает на всей области определения.
- Функция вогнутая при
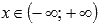 .
. - Точек перегиба нет.
- Горизонтальной асимптотой является прямая y = 0 при х стремящемся к плюс бесконечности.
- Функция проходит через точку (0;1).
Переходим к случаю, когда основание показательной функции больше единицы, то есть, 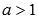 .
.
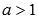 .
.
В качестве иллюстрации приведем графики показательных функций 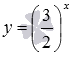 – синяя линия и
– синяя линия и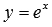 – красная линия. При других значениях основания, больших единицы, графики показательной функции будут иметь схожий вид.
– красная линия. При других значениях основания, больших единицы, графики показательной функции будут иметь схожий вид.
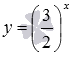 – синяя линия и
– синяя линия и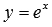 – красная линия. При других значениях основания, больших единицы, графики показательной функции будут иметь схожий вид.
– красная линия. При других значениях основания, больших единицы, графики показательной функции будут иметь схожий вид.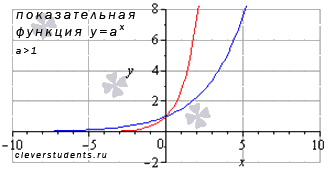
Свойства показательной функции с основанием большим единицы.
- Область определения показательной функции:
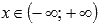 .
. - Область значений:
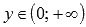 .
. - Функция не является ни четной, ни нечетной, то есть она общего вида.
- Показательная функция, основание которой больше единицы, возрастает при
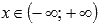 .
. - Функция вогнутая при
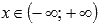 .
. - Точек перегиба нет.
- Горизонтальной асимптотой является прямая y = 0 при х стремящемся к минус бесконечности.
- Функция проходит через точку (0;1).
Логарифмическая функция.
Следующей основной элементарной функцией является логарифмическая функция 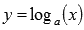 , где
, где 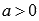 ,
, 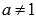 . Логарифмическая функция определена лишь для положительных значений аргумента, то есть, при
. Логарифмическая функция определена лишь для положительных значений аргумента, то есть, при  .
.
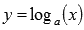 , где
, где 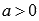 ,
, 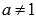 . Логарифмическая функция определена лишь для положительных значений аргумента, то есть, при
. Логарифмическая функция определена лишь для положительных значений аргумента, то есть, при  .
.
График логарифмической функции принимает различный вид в зависимости от значения основания а.
Начнем со случая, когда 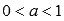 .
.
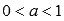 .
.
Для примера приведем графики логарифмической функции при а = 1/2 – синяя линия, a = 5/6– красная линия. При других значениях основания, не превосходящих единицы, графики логарифмической функции будут иметь схожий вид.
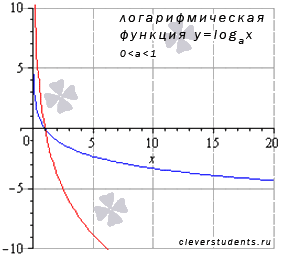
Свойства логарифмической функции с основанием меньшим единицы.
- Область определения логарифмической функции:
 . При х стремящемся к нулю справа, значения функции стремятся к плюс бесконечности.
. При х стремящемся к нулю справа, значения функции стремятся к плюс бесконечности. - Область значений:
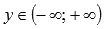 .
. - Функция не является ни четной, ни нечетной, то есть она общего вида.
- Логарифмическая функция убывает на всей области определения.
- Функция вогнутая при
 .
. - Точек перегиба нет.
- Горизонтальных асимптот нет.
- Функция проходит через точку (1;0).
Перейдем к случаю, когда основание логарифмической функции больше единицы (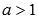 ).
).
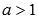 ).
).
Покажем графики логарифмических функций 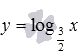 – синяя линия,
– синяя линия, 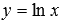 – красная линия. При других значениях основания, больших единицы, графики логарифмической функции будут иметь схожий вид.
– красная линия. При других значениях основания, больших единицы, графики логарифмической функции будут иметь схожий вид.
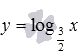 – синяя линия,
– синяя линия, 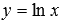 – красная линия. При других значениях основания, больших единицы, графики логарифмической функции будут иметь схожий вид.
– красная линия. При других значениях основания, больших единицы, графики логарифмической функции будут иметь схожий вид.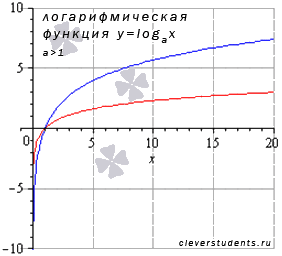
Свойства логарифмической функции с основанием большим единицы.
- Область определения:
 . При х стремящемся к нулю справа, значения функции стремятся к минус бесконечности.
. При х стремящемся к нулю справа, значения функции стремятся к минус бесконечности. - Областю значений логарифмической функции является все множество действительных чисел, то есть, интервал
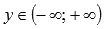 .
. - Функция не является ни четной, ни нечетной, то есть она общего вида.
- Функция возрастает при
 .
. - Функция выпуклая при
 .
. - Точек перегиба нет.
- Горизонтальных асимптот нет.
- Функция проходит через точку (1;0).
Тригонометрические функции, их свойства и графики.
Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.
Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода 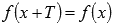 , где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
, где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
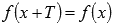 , где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
, где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.
Функция синус y = sin(x).
Изобразим график функции синус, его называют "синусоида".
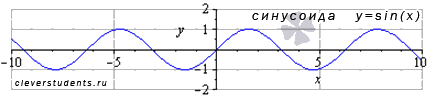
Свойства функции синус y = sinx.
- Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при
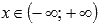 .
. - Наименьший положительный период функции синуса равен двум пи:
 .
. - Функция обращается в ноль при
 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел. - Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть
 .
. - Функция синус - нечетная, так как
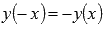 .
. - Функция убывает при
 ,
,
возрастает при .
. - Функция синус имеет локальные максимумы в точках
 ,
,
локальные минимумы в точках .
. - Функция y = sinx вогнутая при
 ,
,
выпуклая при .
. - Координаты точек перегиба
 .
. - Асимптот нет.
Функция косинус y = cos(x).
График функции косинус (его называют "косинусоида") имеет вид:
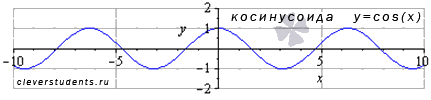
Свойства функции косинус y = cosx.
- Область определения функции косинус:
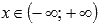 .
. - Наименьший положительный период функции y = cosx равен двум пи:
 .
. - Функция обращается в ноль при
 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел. - Область значений функции косинус представляет интервал от минус единицы до единицы включительно:
 .
. - Функция косинус - четная, так как
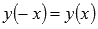 .
. - Функция убывает при
 ,
,
возрастает при .
. - Функция y = cosx имеет локальные максимумы в точках
 ,
,
локальные минимумы в точках .
. - Функция вогнутая при
 ,
,
выпуклая при .
. - Координаты точек перегиба
 .
. - Асимптот нет.
Функция тангенс y = tg(x).
График функции тангенс (его называют "тангенсоида") имеет вид:
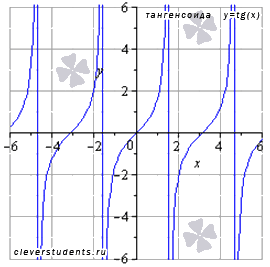
Свойства функции тангенс y = tgx.
- Область определения функции тангенс:
 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
Поведение функции y = tgx на границе области определения
Следовательно, прямые , где
, где  , являются вертикальными асимптотами.
, являются вертикальными асимптотами. - Наименьший положительный период функции тангенс
 .
. - Функция обращается в ноль при
 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел. - Область значений функции y = tgx:
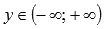 .
. - Функция тангенс - нечетная, так как
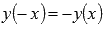 .
. - Функция возрастает при
 .
. - Функция вогнутая при
 ,
,
выпуклая при .
. - Координаты точек перегиба
 .
. - Наклонных и горизонтальных асимптот нет.
Функция котангенс y = ctg(x).
Изобразим график функции котангенс (его называют "котангенсоида"):
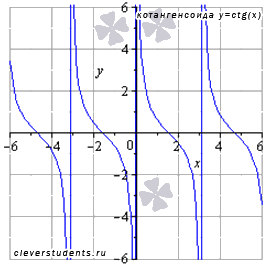
Свойства функции котангенс y = ctgx.
- Область определения функции котангенс:
 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
Поведение на границе области определения
Следовательно, прямые , где
, где  являются вертикальными асимптотами.
являются вертикальными асимптотами. - Наименьший положительный период функции y = ctgx равен пи:
 .
. - Функция обращается в ноль при
 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел. - Область значений функции котангенс:
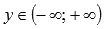 .
. - Функция нечетная, так как
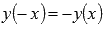 .
. - Функция y = ctgx убывает при
 .
. - Функция котангенс вогнутая при
 ,
,
выпуклая при .
. - Координаты точек перегиба
 .
. - Наклонных и горизонтальных асимптот нет.
Обратные тригонометрические функции, их свойства и графики.
Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки "арк" обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:
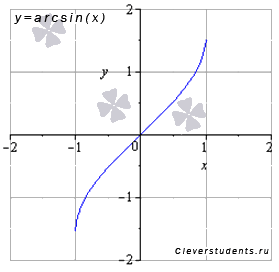
Свойства функции арксинус y = arcsin(x).
- Областью определения функции арксинус является интервал от минус единицы до единицы включительно:
 .
. - Область значений функции y = arcsin(x):
 .
. - Функция арксинус - нечетная, так как
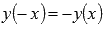 .
. - Функция y = arcsin(x) возрастает на всей области определения, то есть, при
 .
. - Функция вогнутая при
 , выпуклая при
, выпуклая при  .
. - Точка перегиба (0; 0), она же ноль функции.
- Асимптот нет.
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:
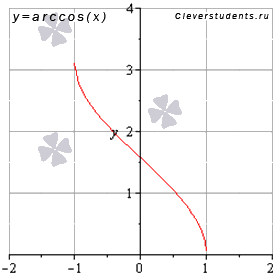
Свойства функции арккосинус y = arccos(x).
- Область определения функции арккосинус:
 .
. - Область значений функции y = arccos(x):
 .
. - Функция не является ни четной ни нечетной, то есть, она общего вида.
- Функция арккосинус убывает на всей области определения, то есть, при
 .
. - Функция вогнутая при
 , выпуклая при
, выпуклая при  .
. - Точка перегиба
 .
. - Асимптот нет.
Функция арктангенс y = arctg(x).
График функции арктангенс имеет вид:
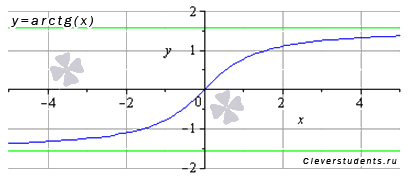
Свойства функции арктангенс y = arctg(x).
- Область определения функции y = arctg(x):
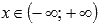 .
. - Область значений функции арктангенс:
 .
. - Функция арктангенс - нечетная, так как
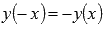 .
. - Функция возрастает на всей области определения, то есть, при
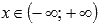 .
. - Функция арктангенс вогнутая при
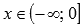 , выпуклая при
, выпуклая при 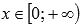 .
. - Точка перегиба (0; 0), она же ноль функции.
- Горизонтальными асимптотами являются прямые
 при
при  и
и  при
при  . На чертеже они показаны зеленым цветом.
. На чертеже они показаны зеленым цветом.
Функция арккотангенс y = arcctg(x).
Изобразим график функции арккотангенс:
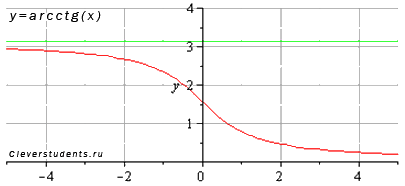
Свойства функции арккотангенс y = arcctg(x).
- Областью определения функции арккотангенс является все множество действительных чисел:
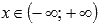 .
. - Область значений функции y = arcctg(x):
 .
. - Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
- Функция убывает на всей области определения, то есть, при
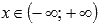 .
. - Функция вогнутая при
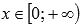 , выпуклая при
, выпуклая при 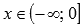 .
. - Точка перегиба
 .
. - Горизонтальными асимптотами являются прямые
 при
при  (на чертеже показана зеленым цветом) и y = 0 при
(на чертеже показана зеленым цветом) и y = 0 при  .
.

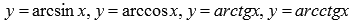
Комментариев нет:
Отправить комментарий